Linear Kid: A mathematical software designed as a computer-based peer tutoring system
Y. Jun
ycjun@sunchon.sunchon.ac.kr
Department of Computer Education
Sunchon National University, Sunchon, Korea
Abstract
The use of computers is increasing in mathematics education. This trend is supported by the NCTM standards and computational power applicable in mathematical curricula. As part of CAI software, Linear Kid was designed, developed and evaluated reflecting upon NCTM standards. Linear Kid is a computer-based peer tutoring system where students become active learners who are guided to learn by teaching a computer. As an intelligent peer tutoring system, Linear Kid has three agents: the student, the computer learner and the computer coach. After the students watch how the computer expert solves a set of linear equations, Linear Kid helps the human student act as a teacher in order to learn more about the subject matter. At this time, the computer plays a role of a student and a coach.
An ongoing version of Linear Kid was tested at two sites in a formative evaluation involving two schools in U. S. A. The evaluation methodology includes analysis of interviews and surveys. Findings indicate that there are diverse qualitative differences among students given several dimensions: (a) types of learning patterns; (b) belief systems and the degree of awareness during problem solving; (c) the use of computers in problem solving; and (d) reactions to the use of Linear Kid. The attitude changes toward the use of Linear Kid imply that practice is not the best way to improve problem solving abilities and that students are not serious about using the property associated with each step in solving linear equations. As a formative process of enhancing educational software, those findings suggests how Linear Kid can be tailored to the students' mathematical learning processes.
Keywords
Problem solving; computer-aided instruction; formative evaluation; peer tutoring.
1. INTRODUCTION
As modern society has moved from an industry-based to an information-oriented structure, life-long learning processes are required for every student. Recently, the rapid development of computer technology brings up changes needed in school curricula not only because society has rapidly changed but because the use of computers has the potential to be applied powerfully in educational settings. All of these situations are well acknowledged by the National Council of Teachers of Mathematics (NCTM). Therefore, NCTM standards [1] were provided in orderr to emphasize the following dimensions in mathematical curricula: (a) problem solving; (b) reasoning; (c) communication; and (d) mathematical connection.
As part of CAI software, Linear Kid was designed, developed and evaluated reflecting upon NCTM standards. Linear Kid is a computer-based peer tutoring system where students become active learners who are guided to learn by teaching a computer. As an intelligent peer tutoring system, Linear Kid has three agents: the student, the computer learner and the computer coach. After the students watch how the computer expert solves a set of linear equations, Linear Kid helps the human student learn more about the subject matter by explaining intermediate problem-solving steps to the computer student. Then, the computer plays a role of a student and a coach.
The goal of this paper is to provide the realization of a prototype learning-by-teaching system and to explore ways of improving Linear Kid based on formative evaluations. Thus, the following questions are posed in this paper: (1) What student learning contexts are related to mathematical problem solving and the use of educational software? and (2) What group differences are there among the students given their problem solving experiences with Linear Kid and their changing attitudes toward Linear Kid?
2. DESIGN AND IMPLEMENTATION OF LINEAR KID
2.1. Background of Linear Kid
2.1.1.Three-Agent Model
The typical educational software adopts a two-agent model: a learning agent (student) and a teaching expert (computer). Linear Kid evolves from a two-agent to a three-agent model. Similar to the conventional CAI, two agents initially communicate with each other in the context of learning by examples. The computer expert demonstrates how to solve problems, and the student imitates and approximates the computer's expertise.
By switching their roles, the system changes into a three-agent model [2]: the student teacher, the computer learner and the computer coach. The computer teacher in the two agent stage steps back and becomes a coach that watches and guides the communication between the student teacher and the computer learner. The human student now takes on the role of a teacher and tries to teach a simulated computer learner. At this point, the knowledge base of the computer learner is treated as a small subset of the expert module. The expert rules that do not belong to the computer learner can be temporarily turned off. These are to be turned on according to the quality of the student teacher's knowledge status. This means that the computer learner has potential expertise which might be superior to the student teacher. In this way, the student teacher can benefit from collaboration with the computer learner and from guidance by the computer coach.
2.1.2. Pseudo Student
Integration-Kid, a Learning Companion System [3] adopts three agents to simulate the students learning with a learning companion (computer companion) and a computer coach. Within this design, the learning companion collaborates with the student while the coach guides both the student and the learning companion agent. For the tasks of solving integration by parts, discourses among those three agents were simulated by a protocol analysis that induced task analysis based on a curriculum tree representation. To mimic the social activities of problem solving, the flow of communication among the three agents is controlled by a scheduler based on a blackboard architecture. In other words, the scheduler determines when and how a human learner is collaborating with a computer peer learner as well as with the computer coachs actions.
On the other hand, a student simulation can be applied to tutoring so that a simulated student can learn from a human tutor. STEPS is such a system which can converse with the tutor in the domain of physics [4]. As inherited from Cascade, STEPS employs a couple of machine learning techniques for explanations of reasoning: Explanation-Based Learning of Correctness [5] and Explanation-Based Generalization [6].
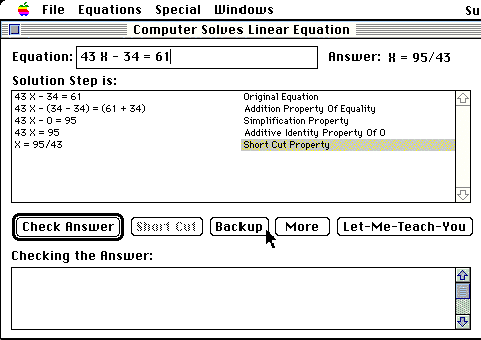
Figure1. Solving Problem mode
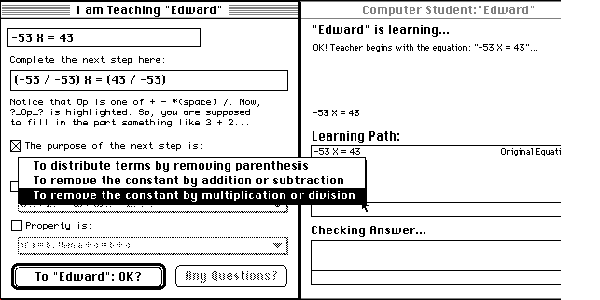
Figure 2. Peer Tutoring mode
2.2. Overall Design of Linear Kid
In Linear Kid, the whole learning environment is comprised of three modes: the Solving Problem Mode, the Guess Answer Mode and the Peer Tutoring Mode. In order to help novice or intermediate-level students gain a thorough understanding of how to solve linear equations, the Solving Problem Mode and the Guess Answer Mode are basically designed as a tutorial. The student watches how a computer expert solves tasks in the Solving Problem Mode (see Figure1). As skill acquisition occurs during problem solving, the student can either go to the Peer Tutoring Mode or go back to the Guess Answer Mode where the student can gain number senses. In the Peer Tutoring Mode, students attempt to demonstrate what they learned in the Solving Problem Mode so that they can learn more by teaching the computer (see Figure2). The student routinely needs to explain the problem solving procedure to the learning agent, and when he gets stuck or explains incorrectly, the computer coach interrupts the student and provides guidance.
3. EXPERIMENTAL DESIGN
3.1. Subjects
For the main data collection, students from two high schools participated in the experiment: School A, a public high school in a medium size city (32 students) and School B, a selective public high school operated by a major university (four students). They used the Linear Kid computer program to improve their proficiencies in solving linear equations and submitted pre-survey and post-survey responses.. Among the 32 subjects, 28 students attended School A students and the rest of them (4 subjects) attended School B. The final pool of 28 School A students split into 15 (53.8%) female and 13 (46.4%) male, ranging from grades 9 to 12.
3.2. Experimental Materials
A short attitude survey consists of 21 items in four categories: mathematical problem solving, explanation, the use of computers and learning patterns. There were five-point Likert scales (5 to 1) for both surveys: (a) Strongly Agree; (b) Agree; (c) Undecided; (d) Disagree; and (e) Strongly Disagree.
Eight subjects were asked to think aloud while they were solving linear equations with Linear Kid. After all of the eight think aloud students finished using the system, they were interviewed to inform the researcher how aware they were of their learning processes and how they reacted to using Linear Kid. In this study the use of interviews is especially critical to reveal any positive or negative feedback toward the system, so that an in-depth analysis of their verbal reports can be geared toward enhancing the system.
3.3. Data Analysis
For the attitude survey data, dependent t-tests for each survey item were used to see if there were any attitude changes during the study. To analyze the interview data, the researcher first attempts to identify what kinds of subject matter are contained in the interview discourses. This approach is primarily adopted to establish structural entities. Second, the researcher tries to summarize the interview data by unfolding its related themes, conceptions and implications.
4. SURVEY DATA ANALYSIS To see whether any changes occurred with the Linear Kid, pre- and post-surveys were used. The reliabilities for the pre-and post- surveys were 0.6118 and 0.7166 respectively, measured by the Cronbach a. For the analysis, dependent two-tailed t-tests were used to compare the means of the paired samples at the .05 level. The result showed that only four items revealed significant attitude changes with the scales from 5 (Strongly Agree) to 1 (Strongly Disagree). Those four significant items are:
Item 3--Solving linear equations is important in school.
Item 7--When I explain to a friend, talking out loud helps me understand how to solve problems.
Item 15--In solving linear equations, it is necessary to know which property (e.g., addition property of equality) supports each step.
Item 19--Practice is the best way to improve ones ability to solve problems.
4.1. Using Properties
From the interview data, some students indicated that they did not necessarily feel the need to use the properties because knowing properties was not crucial for their problem solving. However, knowing the names of properties was different from knowing the meanings of properties. Even though remembering the name of a property was not important, the students felt that understanding a property was sometimes helpful in finding a solution. Notably, many students mentioned that the way they solved linear equations depended on the situations. Interestingly, one subject remembered that she sometimes used to create her own rules rather than relying on ready-made properties. Another subject who was interviewed in the pilot phase mentioned that he used properties such as the Isosceles Angle Property when he proved geometric theorems. However, he rarely used properties while solving linear equations
4.2. Practice
Since the survey results indicate that practice is not perceived as the best way to learn to solve problems, the students seemed to involve constructive processes of building knowledge; even though practice is not a sufficient condition for the mastery of knowledge, it is clearly a necessary component. According to the think-aloud protocols, one subject was not confident of his ability to solve linear equations. He evidently lacked practicing exercises, even though he lost motivation for his mathematical learninghe reflected that he used to be good at algebra. Another view of the interview data suggests that most students seemed to rely on listening to explanations and using examples for their initial knowledge construction processes.
5. INTERVIEW DATA ANALYSIS
5.1. S26 (10th-Grade Girl)
This subject seemed a bit slower than the other subjects and very emotional. Although this subject had difficulty in understanding the instructions for the program, she usually indicated as if she understood the program. She was unfamiliar with using computers for problem solving, although she enjoyed playing computer games. She expressed interest in the computer software to enhance her learning. Throughout the interview, the subject mentioned that she often needed guidance from her teacher's or from her classmates.
5.1.2. Problem Solving
This subject usually solved linear equations without checking answers. It seemed to her that checking answers was sometimes a waste of time. In the real world, however, she felt checking prices was important because prices were changeable when she went shopping.
Like other subjects, using properties did not seem to matter for her finding answers. She seemed to like mathematics, but she was not serious about why she was learning linear equations in school. Probably, she did not have an opportunity to apply mathematics for practical things in school. However, she liked graphical representation of mathematics and creative activities with mathematics. Whichever tools she used, she needed to go through the whole process of solving problems before she could understand it.
5.1.2. Learning Context
Given a task, she usually estimated whether or not she could solve a task. When her teacher explained things or helped her get through several examples until she could understand them, she could learn best that way. When she got stuck during problem solving, she asked her teacher rather than her friends to make sure she found the right answer. Working with her friends was not so helpful for her problem solving since it sometimes took time and distracted her from doing homework. One of the issues she raised was the authority of constructing knowledge in a collaborative mode; where does the authority come from? Even though solving linear equations is well-structured, she believed that the teacher was the only person who could confirm the answers.
Regarding the use of technology, she used a calculator all the time but she seldom used a computer for her learning. It was necessary for her to go through things to see and hear the results. On the other hand, her best learning strategy was the combination of explanation and practicing, but not much memorization. After somebody explained concepts or examples to her, she practiced them for her understanding. Because of such a sequential learning process, she felt a textbook was better for her learning mathematics than a computer.
5.1.3. Reactions to Linear Kid
Unlike the conventional drill software, she appreciated the feedback components of the Linear Kid, which not only signaled the occurrence of errors but provided explanation. In the Peer Tutoring Mode, she complained about the lack of clear instruction on how to use it. Besides, she recommended that the software be equipped with a kind of on-line help system. Overall, she regarded Linear Kid as a teaching game, partly because she liked using game-like software for problem solving. In playing such a game, she seemed to learn more about solving linear equations. This viewpoint brings up important issues on the use of games for the students learning. Even though she did not notice what was going on in the computer students window, she was really excited about seeing an enhanced version of the computer student by using sound and picture. The dimension of emotional motivation seemed to affect her way of using a computer for her problem solving.
5.2. S30 (8th-Grade Boy)
This subject responded readily to all the questions, but sometimes he seemed to falter in his speech. He was a fast learner, and he was very confident in his abilities. He was able to describe immediately how he solved linear equations, and then quickly go to the computer and assert his ideas. The subject was very logical and analytical in his approach.
5.2.1. Problem Solving
He was capable of solving most linear equations. When he looked at the tasks he first mentally kept track of problem solving paths and checked how the system proceeded to find answers. Because of problem complexity, he preferred dealing with constant numbers first to remove them when he solved linear equations. He further recognized that the order of doing certain computations does not matter. Thus, he tried to reduce the problem task to a simple form. When he solved linear equations he did not use or even remember property names, but he mentioned the importance of using them. He usually skipped steps and easily carried out simple mental calculations. Even though he did not like checking answers he mentally checked answers if necessary.
Like other fast learners, he was very confident in his problem solving skills and made almost no errors. And, he did not care about the possibility of learning from errors. However, he noticed several occasions where he could not avoid making errors because of several constraints such as time and effort involved with problem solving. He was pretty aware of how problems could be solved. When he solved linear equations he usually monitored what he was doing. Again, he was confident in his problem solving skills. Moreover, he believed mathematics helped him make better decisions in real situations, such as playing poker.
5.2.2. Learning Context
When he learned new problems or subjects, the use of properties or formulas helped him initiate searching for answers. Given problems, he tried to figure out how to find answers by himself, even though he realized the need of collaboration with his friends while solving very difficult problems. His view indicated that his fast and easy learning often resulted from his own efforts to figure out everything. Considering himself a quick learner, he was proud of his fast learning capability. He did not seem to benefit from talking aloud at all when he explained things to others. Overall, practicing was not a good way for him to learn mathematics because it was too slow.
In school, he usually listened to his teacher, tried to understand her explanations and got some help for solving problems. Most of the time, he learned mathematics in the classroom and did not seem to use a computer much. Thus, he was not sure of a computers capability to facilitate his learning even though he indicated such a possibility. Rather, he pointed out that it took a while to get used to working with a computer before he could take advantage of the computer for his own learning.
5.2.3. Reactions to Linear Kid
For the Solving Problem Mode, he thought the program was useful for both beginning and experienced students; novice learners need to learn in a step-by-step fashion while experienced students need to shorten problem solving steps. About the Peer Tutoring Mode, he thought it was not important to use the purpose of the next step, even though it might be useful for others. According to him, advanced students might not use demonstrating purposes, explanations and examples but beginners would use them. As for the realistic computer student, the fidelity of the computer student did not matter for his learning at all. Even though the computer student could be enhanced by the addition of sound or picture, such an additional feature might be a distracting factor for his learning process. Instead, he suggested that the computer student carry on a normal kid's verbalization.
6. DISCUSSION
6.1. Problem Solving
Within the problem solving dimension, there was a big difference between strong and weak linear equation solvers. Experienced students who already knew how to solve linear equations often complained that the system was too slow; it generated too many steps and too much confirmatory feedback. Such slowness seemed to hinder their problem solving. As expected, however, low-level students welcomed the system because it guided them with very detailed feedback through buttons and menus. In this way, detailed descriptions of solution steps were most beneficial for their understanding on how to solve problems.
On the other hand, there were diverse types of students for the meta-cognitive aspects of problem solving. Some students consciously monitored their problem solving; a few seemed to automate their solution steps without explicit monitoring. Slow learners were not eager to follow up their problem solving steps by searching for answers. In a well-structured domain such as solving linear equations, most subjects did not attempt to use the menu which was designed to facilitate comprehension monitoring with the following menu items: Summarize..., Frequently Asked Questions and Predict... (refer to reciprocal teaching methods, Palincsar & Brown, 1984). There are two ways to interpret this phenomenon. First, the subjects did not have enough time to try those menu items. Menus are treated as high-level objects whereas buttons are more easily accessed by novice students. Second, reciprocal teaching activities were organized and anchored in reading comprehension, which is not a well-structured domain. This might imply that solving linear equations is not directly influenced by activities such as summarizing, predicting and asking questions.
The students belief systems were diverse as well. While some students merely thought there was no relationship between mathematics and the real world, other students saw various connections between the two worlds. For instance, a couple of students preferred applying mathematical concepts to creative activities, and others recognized the necessity of learning to solve linear equations as a building block in a mathematical system.
6.2. Learning Contexts
The use of computers for mathematics varied from person to person. Some subjects did not like using computers for their mathematical problem solving. This phenomenon led them to feel indifferent about benefits of computer usage. Instead, they were accustomed to solving problems without computers, but they indicated that it might be useful to employ computers for computational intensive tasks such as statistics. On the other hand, students who liked using computers expressed positive attitudes towards working with Linear Kid. They were fond of solving linear equations in the Solving Problem Mode, and they appreciated the step-by-step problem solving fashions as well as the feedback components. Unfortunately, there were only a few subjects who used computers for learning mathematics.
Most students relied on explanations and the use of examples when they initially acquired new mathematical knowledge; when somebody explained concepts and illustrated how each example represented underlying concepts, the students seemed more likely to understand. Such patterns of acquiring knowledge lead CAI developers to emphasize providing explanatory feedback and facilitating relevant examples for a given task at hand. A couple of other students indicated that they were willing to explore or to experiment with ideas and concepts.
It was also found that there were two types of learning patterns among individuals. Some students preferred working by themselves at their own pace. One of the reasons why they disliked collaborating with their friends was that they were easily distracted. Thus, they might not progress as they should. Those students did not like explaining concepts or demonstrating examples to the computer student in the Peer Tutoring Mode. Yet, there was another group of individuals who benefited from collaborating with each other for problem solving. Those students clearly recognized the importance of debating or explaining relatively hard problems.
6.3. Suggestions for Linear Kid
For the most students, the use of properties in solving linear equations was not necessary in the Solving Problem Mode. The Peer Tutoring Mode was too slow for fast learners who did not find the use of pop-up menus helpful for fostering comprehension and explanation. Accordingly, it turns out to be necessary to enhance the system.
It was also noticed that human peer tutoring is quite different from a human learner's point of view than from the artificial peer tutoring that was implemented in the current system. One critical point arose from the lack of a detailed on-line help system, even though Linear Kid was equipped with short text-based directions. Several students suggested the addition of realistic conversation, picture, sound and even color to the computer student. Many students commented that playing a game was fun and mathematics was boring, which implied Linear Kid could be considered game-like software.
6.4 Summary
First of all, this study's findings indicate that there is still a gap between the student-oriented learning processes and the use of technology-oriented learning tools. The patterns of student learning are very dynamic, but driven by the conventional and rigid school-based communication. Notably, students seldom appreciate the use of computers in mathematics learning. Furthermore, some students do not benefit much from shared communication because they do not necessarily communicate with each other when solving linear equations. However, many students seem to recognize the importance of connecting mathematical ideas across different subject areas, while others are aware that it is critical to master basic building blocks such as linear equations to get into the upper levels of mathematical abstractions. Thus, the Linear Kid needs to be enhanced as a tool for individulized learning environments by taking into account individualized differences in mathematical problem solving.
References
[1] National Council of Teachers of Mathematics. "Curriculum and evaluation standards for school mathematics," NCTM, 1989.
[2] S. Card, "Human factors and artificial intelligence," In P. A. Hancock & M. H. Chignell (Eds.), Intelligence interfaces: Theory, research and design (pp. 27-48), North-Holland, 1989.
[3] T. W. Chan, "Learning companion systems," Unpublished doctoral dissertation, University of Illinois at Urbana-Champaign, 1989.
[4] S. Ur and K. VanLehn , "STEPS: A preliminary model of learning from a tutor," Proceedings of the Sixteenth Annual Conference of the Cognitive Science Society, 1994, pp 893-888.
[5] K. VanLehn and R. M. Jones, and M. T. H. Chi, "A model of the self-explanation effect," The Journal of Learning Sciences, 2, 1991, pp 1-59.
[6] T. M. Mitchell, and R. Keller, and S. Kedar-Cabelli, "Explanation-based generalization: A unifying view," Machine Learning, 1, 1986, pp 47-80.
[7] A. S. Palincsar, and A. L. Brown, "Reciprocal teaching of comprehension-fostering and comprehension-monitoring activities," Cognition and Instruction, 1(2), 1984, pp 117-175. v
[8] L. B. Resnick, "Treating mathematics as an ill-structured discipline," In R. I. Charles & E. A. Silver (Eds.), The teaching and assessing of mathematical problem solving (Vol. 3, pp 32-60), NCTM, 1988.
[9] A. H. Schoenfeld, "Beyond the purely cognitive: Belief systems, social cognitions, and metacognitions as driving forces in intellectual performance," Cognitive Science, 7, 1983, pp 329-363.
[10] A. H. Schoenfeld, "Making sense of "out loud" problem-solving protocols," The Journal of Mathematical Behavior, 4, 1985, pp 171-191.
[11] J. W. Schofield and D. Evans-Rhodes and B. R. Huber, "Artificial intelligence in the classroom: The impact of a computer-based tutor on teachers and students," Social Science Computer Reviews, 8(1), 1990, pp 24-41.
© Asian Technology Conference in Mathematics, 1997.
|