The Joy of Creating Virtual Mathematical Sculptures
Jen-chung Chuan
Department of Mathematics
Tsing Hua University
Hsinchu, Taiwan
jcchuan@math.nthu.edu.tw
The process of turning symbols into a mathematical sculpture has never been easier! This is what you need:
- a copy of Maple V release 5.
- a web browser configured with a VRML plugin such as the Cosmo Player.
Maple V furnishes the computing environment allowing you concentrating on the mathematical formulation while silently taking care of the nonmathematical procedures needed in the visualization. Cosmo Player, on the other hand, creates the kind of visualization environment letting the users to experience the thrill of manipulating virtual geometric objects by rotating, by dragging and by zooming.
Building virtual 3D models creates many fruitful learning activities. We find the following examples particularly exciting.
Villarceaux circles
Here is a sculpture which embodies an important mathematical idea: through every point on a torus, there are four circles passing though it!
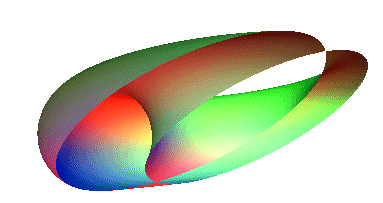A complete, rigorous proof of this fact can be found in "Invitation to Geometry" written by Z.A. Melzak[2]. This interesting geometric phenomenon was discovered in 1848 by M. Villarceaux.
It takes seven lines of Maple commands to create such an object:
> a:=3;b:=7;c:=sqrt(a^2+b^2);
> r:=c+a*cos(t);
> x:=r*cos(s);
> y:=r*sin(s);
> z:=a*sin(t);
> u:=solve(b*z=a*x,s);
> plot3d([x,y,z], s=-u..u, t=0..2*Pi, scaling=constrained, grid=[30,80]); |
Assuming the symbol h stands for the process of drawing the object:
| > h:=plot3d([x,y,z], s=-u..u, t=0..2*Pi, scaling=constrained, grid=[30,80]): |
The conversion of the geometric object into the required VRML file is now straightforward.
| >vrml(h,"d:/vrml/villarceaux.wrl", background_color=white); |
As a related question, one might ask if a half-torus can have a boundary consisting of two disjoint interlocking circles? The answer: yes, just choose a Villarceaux circle of any torus as a generator of the half-torus and rotate it by 180 degrees about the axis.
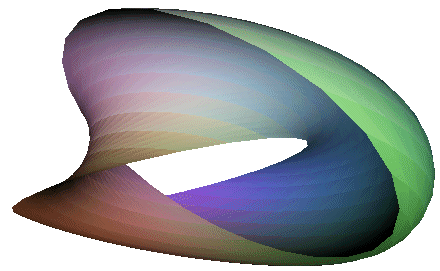Here is the associated code:
> a:=3;b:=7;c:=sqrt(a^2+b^2);
> x1:=b*cos(t);
> y1:=a+c*sin(t);
> z:=a*cos(t);
> x:=x1*cos(u)-y1*sin(u);
> y:=x1*sin(u)+y1*cos(u);
> plot3d([x,y,z],u=0..Pi,t=0..2*Pi,scaling=constrained); |
Knots
Knot theory involves the embedding of the unit circle into three-dimensional space. Under Maple V, the visual representation of a knot becomes straightforward when the command "tubeplot" is used. For example, the following procedure in Maple:
> r:=3+cos(t);
> x:=r*cos(s);
> y:=r*sin(s);
> z:=sin(t);
> s:=2/5*t;
> tubeplot([x,y,z], t=0..10*Pi, radius=0.6,scaling=constrained, grid=[100,10]); |
generates a torus knot as in this illustration
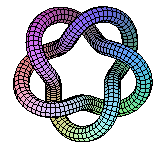By readjusting the ratio between the parameters s and t, we produce this:
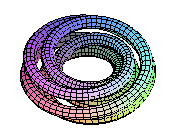
Problems taken from the Calculus textbooks
Here is a typical problem that appears in a calculus textbook:
Find the volume of the region common to the interior of the cylinders
x2 + y2 = a2 and x2 + z2 = a2. |
The solid looks like this:
The boundary of the solid consists of two parts: the first part may be created with this code:
> u:=[cos(t),sin(t),sin(t)];
> v:=[cos(t),sin(t),-sin(t)];
> w:=expand((1-s)*u+s*v);
> plot3d(w, s=0..1, t=0..2*Pi, scaling=constrained, color=green); |
while the second part is obtained by rotating the first:
| > plot3d([w[1],-w[3],w[2]],s=0..1, t=0..2*Pi, scaling=constrained, color=yellow); |
Realizing the parametric description of the solid is the most difficult part in solving the original problem. If we examine how the surfaces are represented symbolically, we find exactly what is need: the cross-sections perpendicular to the x-axis consist precisely of squares with u, v, -u and -v as corners. This serves as an example in which a clear visual understanding of the problem leading to a clear analytical solution.
The following example is taken from p. 988 of the 7th edition of Thomas/Finney Calculus[5]:
| Find the volume of the three-dimensional region enclosed by the surfaces
z = x2 + 3y2
and
z = 8 - x2 - y2.
|
There is a neat picture in the text accompanying the example illustrating the region in question. It is a static picture; the reader has to be persuaded that the two surfaces intersect on an elliptic cylinder from this one single snapshot. Can we have a view of the region from all directions? Yes, it is possible, with Cosmo Player. This is what is required:
> xx:=2*cos(t);
> yy:=sqrt(2)*sin(t);
> x:=s*xx;
> y:=s*yy;
> z:=x^2+3*y^2;
> h1:=plot3d([x,y,z],s=0..1,t=0..2*Pi,scaling=constrained, color=green,grid=[20,50]):
> z:=8-x^2-y^2;
> h2:=plot3d([x,y,z],s=0..1,t=0..2*Pi,scaling=constrained, color=red,grid=[20,50]):
> h:=display(h1,h2):
> vrml(h,"d:/history/cal.wrl",background_color=white); |
and this is a snapshot of the resulting VRML file:
The perspective appears quite differently from that in the text.
Here is another similar challenging calculus problem:
| Find the volume of the region common to the interior of the intersection of the cylinder (x - 0.5)2 + y2 = 0.25 and the sphere x2 + y2 + z2 =1. |
Again, the vexed question is: "What does the solid region looks like?" Since a part of the boundary lie on the unit sphere, the attention is thus turned to the spherical coordinates. The Maple V commands used to describe the region is in fact a direct translation of the related mathematical formula:
> r:=cos(s);
> x:=r*cos(t);
> y:=r*sin(t);
> z:=sin(s);
> a1:=plot3d([x,y,z],t=-s..s,s=0..Pi/2,scaling=constrained, color=red,grid=[100,10]):
> a2:=plot3d([x,y,-z],t=-s..s,s=0..Pi/2,scaling=constrained, color=red,grid=[100,10]):
> t:=s;
> b:=plot3d([x,y,(1-2*u)*z],u=0..1,s=0..Pi, scaling=constrained, color=red,grid=[10,100]):
> display(a1,a2,b); |
Variation on the theme of Platonic solids
Maple V has a built-in library comprising the five Platonic solids and many, many more interesting polyhedra ready to be invoked. We find it interesting to build virtual models fulfilling the same spatial symmetry as the Platonic solids.
 
 
 
 
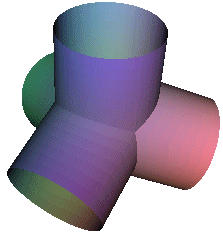
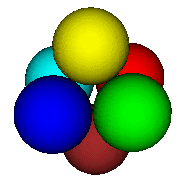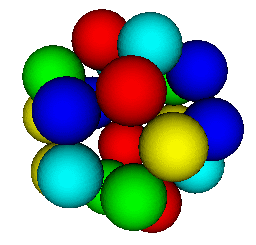
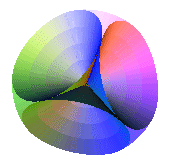To form the whole structure, we proceed by building up a small "fundamental" piece and then simply apply the Maple commands "rotate", "reflect" or "translate" to form the rest and then paste everything together with the "display" command.
Sphere
Although living on the surface of the earth, we usually draw pictures and diagrams on a flat piece of paper. How does it feel like drawing on a sphere? What interesting ways can we partition a sphere? It's surprising how little visual feeling we have for such a very common mathematical object. Yes, sooner or later we have to go back to the plane and make transformations to the sphere.
   
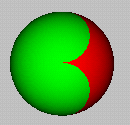
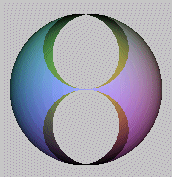
Ruled surfaces
The hyperboloid of one sheet can be regarded as a ruled surface. If we are to build one one-half of the surface
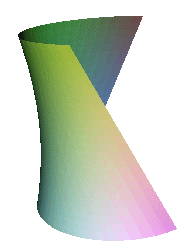reflect it across one straight line generator and glue the two pieces together, this interesting new ruled surface appears:
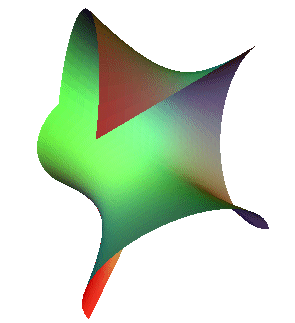Does this sculpture reminds you of another classical sculpture?
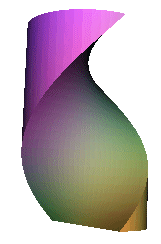It is simply a right helicoid mimicked after the illustration on D. Struik's Lectures on Classical Differential Geometry[4]. By rotating and translating at the same time on a regular triangle, we obtain this ice-cream like object:
If the same operations are performed on a square, a cake-topping is formed:
Orthogonal grids
There are not many surfaces on which we are able to perform exact computation and draw geodesics, except the flat plane, the cone, the cylinder and the sphere. By taking the stereographic projection
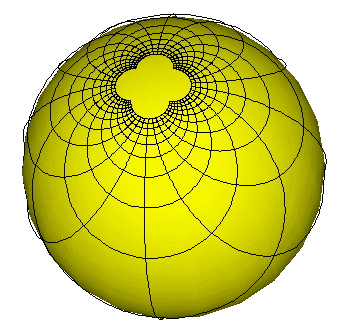
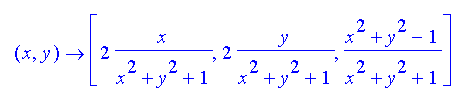we are able to draw orthogonal grids consisting of circular arcs on a sphere:
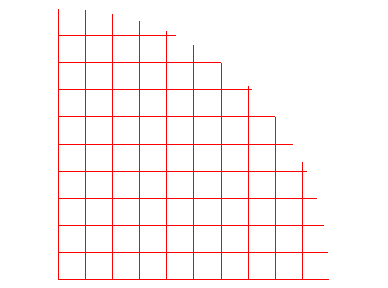
After the idea mentioned in Steinhaus' book[3], by wrapping around the usual Cartesian grids such as
we form this orthogonal grids on a cone:
Similarly, these grids
are transformed into
and
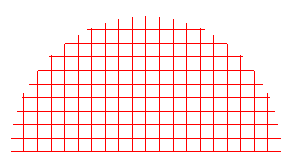into this:
You are invited to examine the Maple code used in creating these objects in
http://poncelet.math.nthu.edu.tw/chuan/exp99/14/cone2.mws
References:
- H.S.M. Coxeter, Regular Polytopes, Dover, 1973.
- Z.A. Melzak, Invitation to Geometry, Wiley, 1983.
- H. Steinhaus, Mathematical Snapshots, Oxford University Press, 1983.
- D.J. Struik, Lectures on Classical Differential Geometry, Addison-Wesley, 1950.
- G.B. Thomas and R.L. Finney, Calculus, 7th Edition, Addison-Wesley, 1988.
© 1999. ATCM, Inc. |
